之前对分类Classification问题只有浅显的理解,最近认真学习了Classification问题的两种解决思路,比较了Generative和Discrimitive两种模型的异同,同时也学习了模型的一些细节与问题处理。另外从Logistic Regression到Neural Network的过渡也让我印象深刻,深度学习真的很有魅力!
Generative Classification(产生式模型)
解决分类问题的一个思路是,能不能套用回归问题?例如,二分类问题,设第一组的y^为1,第二组的y^为-1,然后去回归拟合一条直线来区分两类数据,可不可行?这种思路的代表方法如Fisher线性函数法。但这种区分函数法有很大问题。比如,如果在y^为1的一组中,存在距离很远的一组数据,值远大于1,这样拟合这些数据会使得直线进行倾斜,从而影响分类准确率。
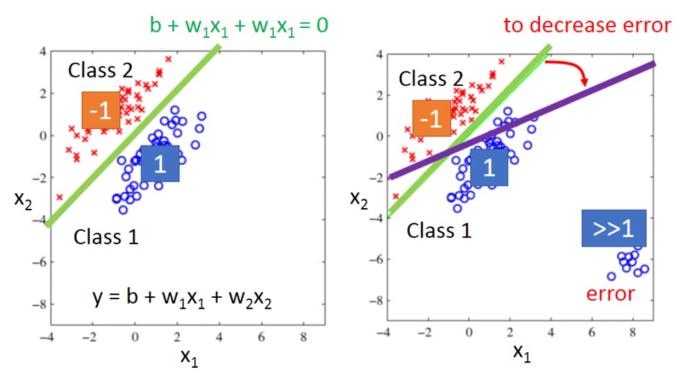
为了解决分类问题,需要转变思路,于是提出了Generative模型(产生式模型):
Generative意思是要先考虑分布,然后从概率的角度去计算后验概率,用后验概率来分类,属于正向推理。
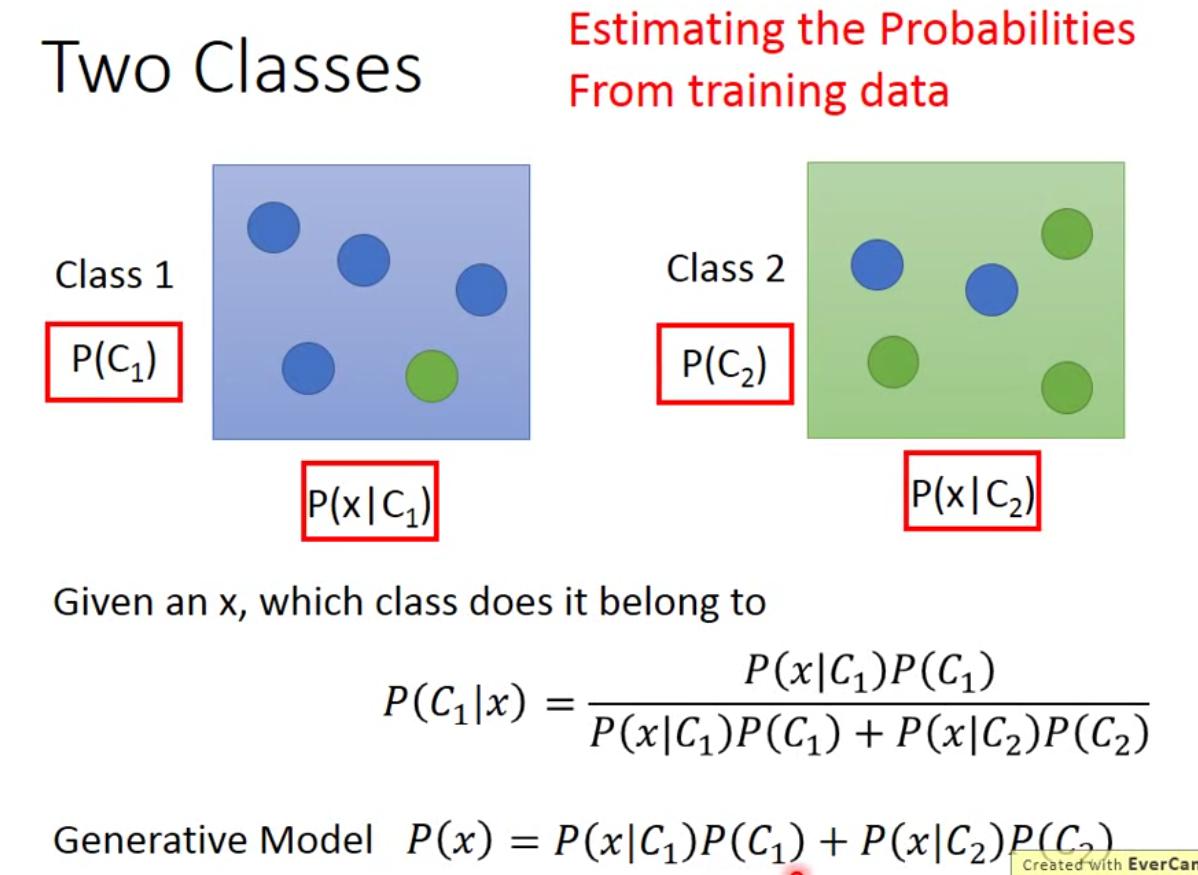
首先考虑贝叶斯公式,为了得出后验概率P(C1|x),要分别计算先验概率prior probabilities如P(C1)等,以及class-dependent probabilities如P(x|C1)。
这些值可以从我们的training data中得出:例如先验概率可以直接按照数据量计算,而class-dependent概率需要做假设。假设数据满足某分布,比如满足高斯分布Gaussian distribution,那么可以根据数据找出该高斯分布的两个指标,均值向量μ和协方差矩阵Σ。
怎么找呢?用最大似然,可以直接代入公式算。
得出指标之后可以代入class-dependent概率的公式,再和先验概率一起代入就可以得到后验概率的函数。
然而,这样的generative模型有个问题是由于高斯分布的参数比较复杂,分类准确率不高。可以通过两个类的高斯分布共享同一个协方差矩阵的方式来解决。假设两高斯分布的协方差相同,仅仅是均值不通,即Σ1=Σ2取加权平均,这样分类的时候boundary就是线性的了,参数少一点,会更准确。
总思路如下:

其实,分布也可以选用其他分布,对于二分的feature完全可以采用贝努利分布。
另外class-dependent概率P(x|C1)中x是一个一维向量,所以后验概率还可以拆解成多个x1,x2,x3,然后概率相乘,进一步简化模型。这样做的前提是各个dimension满足独立分布,这就是朴素贝叶斯。
Generative模型还可以深入推敲。后验概率可以提出一个参数z,然后用sigmoid函数表示:

经过数学运算,z最终可以表示成Wx+b的形式,那么我们可以考虑,不要用复杂的概率模型,也不要去计算μ和Σ,直接通过数据去训练更新权重W和偏差b可以吗?这就引入了另一种解决分类问题的模型,Discrimitive模型(判别式模型)。
Discrimitive Classification(判别式模型)
Discrimitive模型的思路是,既然最终后验概率可以转化成用w和b作为参数表示的形式,为什么不直接用数据去更新w和b呢?这样的思路和回归问题更加接近。设计loss函数的时候,思路和之前的产生式模型类似,也是用最大似然maximum likelihood,用现有的training数据去拟合最可能的分布。设计第一类的y^为1,第二类的y^为0,这样的话Loss函数可以用训练数据和ground truth的交叉熵来表示(可以直接推导)。

最后一步是通过目标函数求微分来计算梯度更新W,可以对比发现这一步更新weight的梯度公式和linear regression是一样的。

那么为什么在step2中,逻辑回归的损失函数用交叉熵表示而不用方差呢?可以通过下面的图直观地看出来。如果用方差的形式来表示logistic regression的损失函数,那么在求梯度的时候会遇到远处梯度为0的情况,而且作图也可以看出来loss下降的曲线斜率也明显有差别。
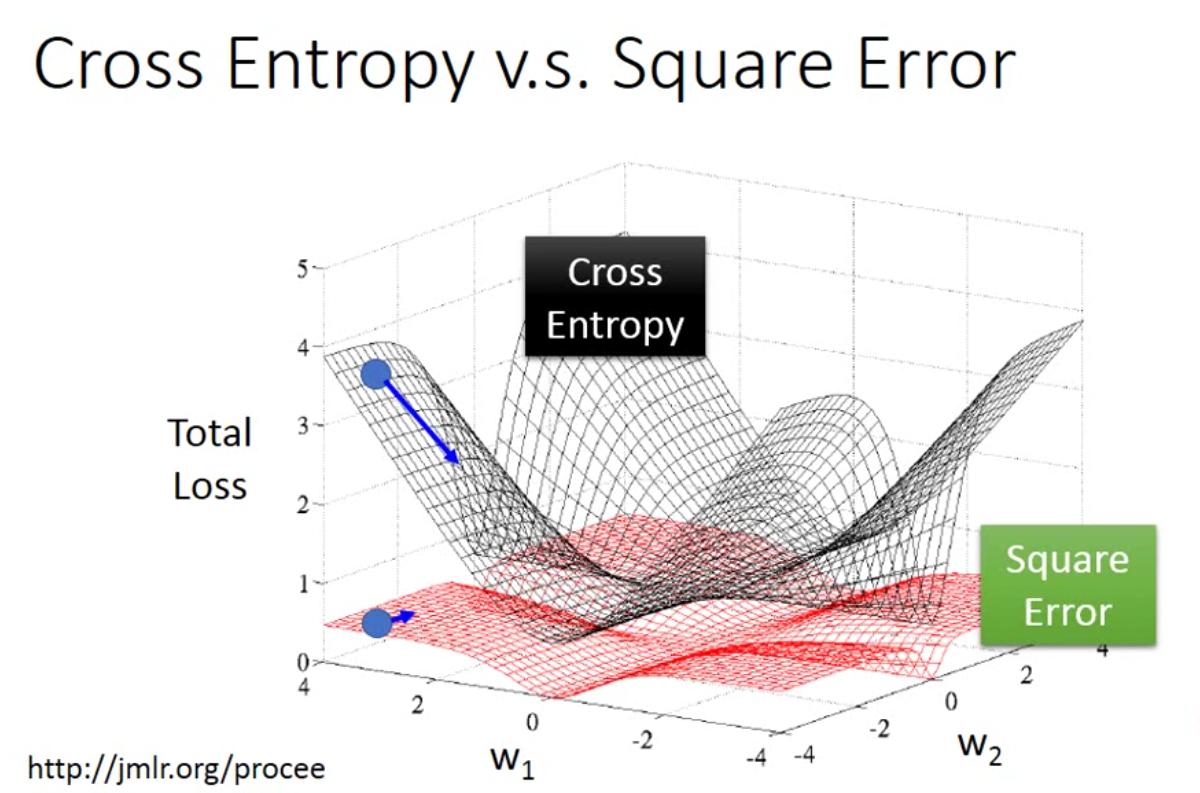
Generative vs Discrimitive
G和D的两个模型对比来看,Discrimitive的模型往往是更加准确的,因为G其实会脑补出一些数据的分布情况,我们利用G的同时其实也会默认提出一些假设,比如满足高斯分布,满足伯努利分布(Bernoulli distribution),满足独立性(朴素贝叶斯)等等;另外在计算后验概率的时候,G会更加看中已经有的数据样本,会受采集样本分布的影响,导致出现一些问题。
当然G也有一些好处,比如基于概率分布的假设时,需要的数据更少(可以脑补);面对噪音更加稳定;同时,先验概率priors和class-depedent概率可以分开计算,可以来自不同的数据源了(例如语音辨识虽然是用了神经网络,但还是离不开Generative的大框架)
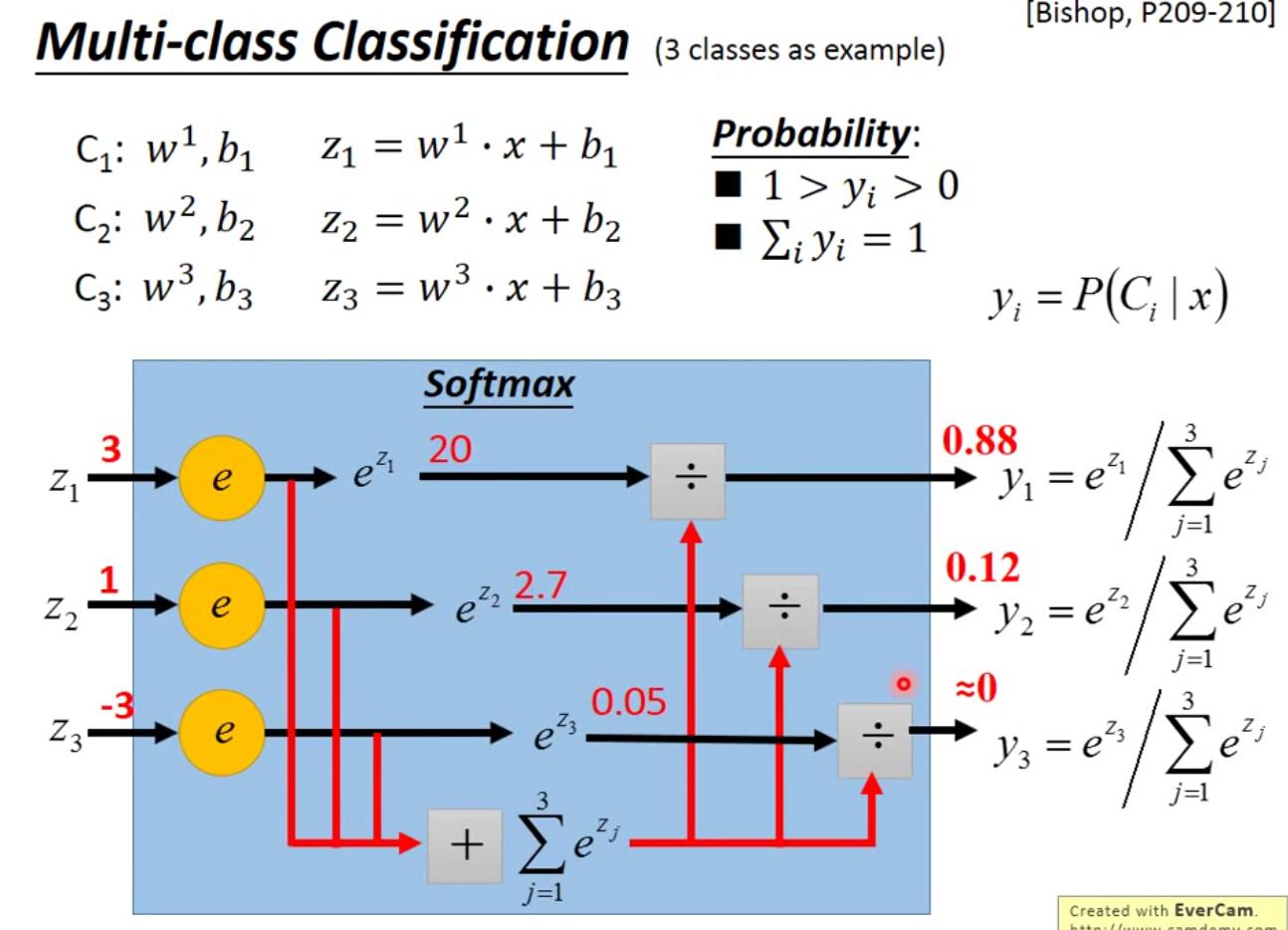
Multi-class Classification
对于多类别分类问题,考虑用softmax方法处理输出。每个类对应一组w和b,输入的x经过线性变换和softmax处理后直接输出分在该组的概率(后验概率),训练的话仍使用交叉熵作为损失函数。另外,目标的表示方法也由0-1表示变成了one-hot表示。
How to make it Deep?
逻辑回归也有其局限性。Logistic Regression分类的boundary是线性的,导致有些数据交叉分布时没有办法分开,需要用到feature transformation的方法,将数据重新分布后再做逻辑回归。但是这样还是比较复杂,很难有确定的feature transformation的方法。
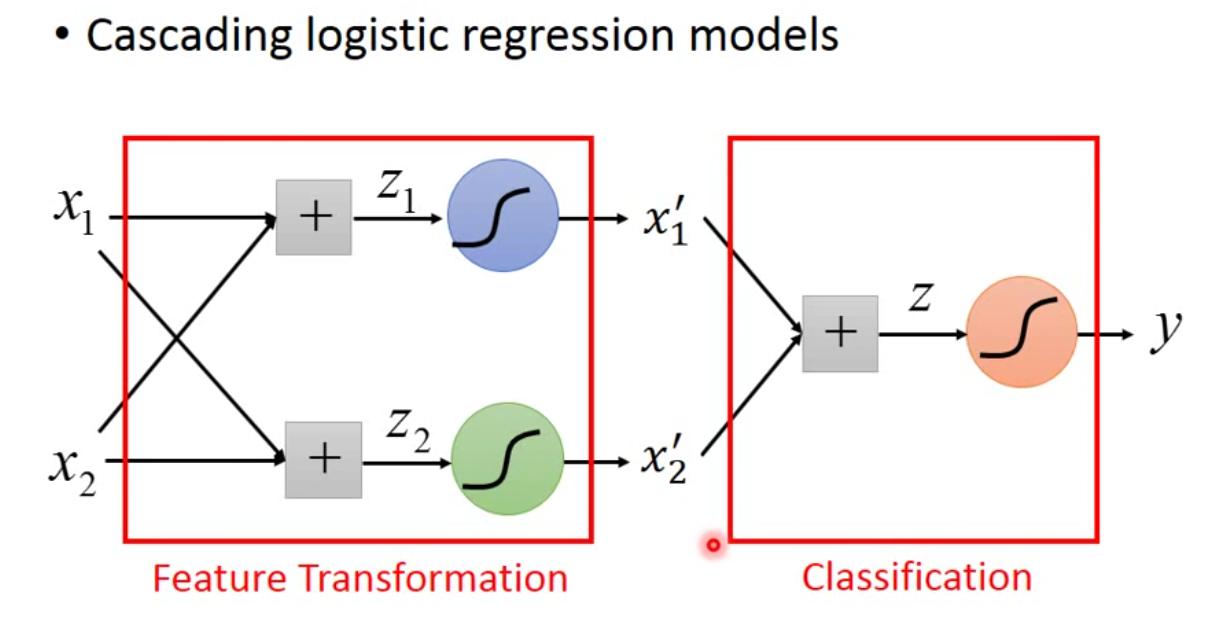
可以cascading logistic regression models,将逻辑回归模型拼接起来,这样用前面一层的逻辑回归对数据进行重新分布,再用后一层的模型对数据进行分类。这样多个相连,我们把每个logistic regression模块叫做一个neuron,这样整个网络就变成了neural network,就发展成了deep learning。
More About Maximum Likelihood
在Logistic Regression的推导过程中,运用了最大似然估计的方法,其实回过头去思考已经学习过的Linear Regression,也可以从这个方法中得到新的收获。
例如,为什么线性回归的误差函数是用平方误差来表示?我们知道线性回归中y与t存在差别,是因为观察值t拥有随机性,我们假设这一随机性符合一个以0为均值、β^(-1)为方差的高斯分布,那就可以得到线性回归模型生成所训练数据集的总概率。我们想要使自己的线性模型拟合得最好,也就是要使我们的模型生成这一数据集的概率最大,即最大化似然函数。通过计算似然函数可知,为了最大似然,式中第三项需取最小,也就是说最大似然估计等价于线性拟合。

此外,到目前位置我们讨论各种对应关系、数据分布假设时都是基于最大似然准则,即模型对训练数据的概率最大化。但是有些情况下,也会有其他的考虑。例如我们经常希望将知识和数据结合在一起,这时候就不仅仅要考虑训练数据概率最大化,还要考虑先验知识在目标函数中的比重,这时的准则就不再是最大似然,而是最大后验(Maximum A Posterior, MAP)。事实上,需要根据不同的数据分布情况选择恰当的模型。